债市流动性框架之一：如何测算超储率？

　　摘 要

　　近几个月资金面有所收敛，债市投资者对超储率关注度有所上升，8月超储率可能降至1%左右。本文给出一种可行的月度超储率测算方法。

　　测算超储的必要性：接近“银根”的指标。对于银行而言，基础货币之中，超额准备金和库存现金属于可动用的资金，一般情况下法定准备金被央行冻结无法动用，流通中现金则由金融体系以外的机关、部队、企业和个人所持有。因而，银行可动用的资金主要是超储，其次是库存现金。相对于基础货币，超储更为接近商业银行的“银根”属性。

　　超储率测算的一般方法。以央行发布的季末月超储率为基础（假设为t月），加上估算得到的超储率月度环比变动，即可得到下一季度季初月（t+1月）和下一季度季中月（t+2月）的超储率，同样也可递推下一季度季末月（t+3月）的超储率，待延后发布该数据后进行印证。

　　定向降准等情况下测算超储率的特殊处理。今年3月央行普惠金融定向降准；4月和5月针对中小银行定向降准，测算时需要对法定准备金率变动进行还原，否则会将法定准备金率调整引起的变化，纳入到超储变化。需将这种实际上是法准的变化加回去，才能得到真实的超储率。

　　与五因素方法的对比：误差相对较小。五因素绝对额估算产生的误差往往更大，一方面原因是忽略了再贷款等因素的影响。另一个原因在于我们测算方法中先计算准备金率再差分，这种求比例环比变动，可以在差分中规避五因素方法中其他项因素的扰动。

　　根据我们的测算方法直接计算超储率环比变动时，用同一变量对应的不同统计指标测算得到的结论相差无几。甚至在缺失部分指标时，也可以对超储率变动进行近似计算。

　　超储率的应用：分析中期资金面。超储率具有季节性特征，将当前月份的超储率，与历史同期超储率进行比较，例如去年同期、资金面较为紧张或宽松的年份同期，可以得到中期资金面的一个初步判断。

超储率作为月频数据，对于月内资金面的波动“束手无策”，但可以作为分析起点。月内资金面的波动却没办法由月度超储率的一个时点值来捕捉。分析月内资金面的变化，需要根据影响资金面的日度数据作进一步分析，而超储率恰恰可以作为月内流动性分析的起点。

　　核心假设风险。测算超储率所使用的指标出现口径调整。

　　近几个月资金面有所收敛，债市投资者对超储率的关注度有所上升，8月超储率可能降至1%左右。央行发布的超储率数据为季末月值，那么作为季初月、季中月超储率如何测算？本文试图给出一种可行的月度超储率测算方法。

　　1

　　测算超储的必要性：接近“银根”的指标

　　MLF超量续作，背后是超储率降至2017年水平MLF超量续作，背后是超储率降至2017年水平MLF超量续作，背后是超储率降至2017年水平

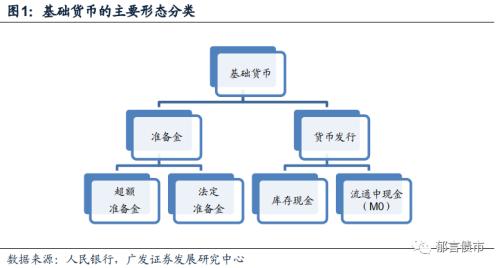
　　超储和基础货币的关系：超储，即超额准备金，是基础货币中准备金存款的一部分。基础货币包含准备金和货币发行两部分。其中准备金又包括法定准备金和超额准备金，超额准备金是超出法定准备金的额外准备金存款，两者均以准备金存款的形式存放于央行。货币发行包括流通中现金M0和商业银行的库存现金。

　　就规模而言，2020年8月基础货币为29.8万亿（货币当局资产负债表中的基础货币）；货币发行8.5万亿元（货币当局资产负债表的储备货币中的货币发行），包含M0 8.0万亿元，库存现金（其他存款性公司资产负债负债表的储备资产中的库存现金）5392亿元；准备金存款20.0万亿元（其他存款性公司资产负债负债表的储备资产中的准备金存款），法定准备金和超额准备金没有直接对应的指标。

　　除春节月外，库存现金波动相对较小。对于商业银行而言，库存现金主要是为了应付日常的现金收支活动而保存的纸币和硬币，而现金需求主要是传统节日春节所在月份较高。如果剔除春节月，那么可以发现库存现金的波动幅度相对较小，以2019年为例，剔除春节月之后的库存现金最大值和最小值差距在1008亿元，约占最小值的18.8%。这一点说明，银行动用库存现金受到一定程度的约束，不太可能动用20%以上的库存现金。

　　超储的波幅要大于库存现金。相比之下，超储可由银行自主动用，其存量也由银行自主决定。从央行发布的季度超储率数据来看，1年之内超储率的波动有时大于1%，相当于2010年以来超储率均值1.94%的一半左右。这也就意味着银行可以动用超储的50%。

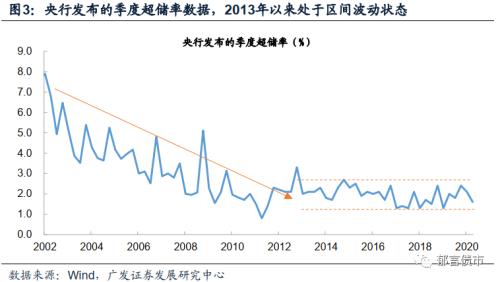
　　超储率指标，根据商业银行超过法定存款准备金而保留的准备金占存款比例计算得到。央行发布的季度超储率指标，一般来源于每个季度的货币政策执行报告中，也就是每年的2月、5月、8月、11月发布上一季度末的超储率。在2017年二季度货币政策执行报告的专栏一中，央行解释了2001年以来超储率趋于下行的原因，主要是三个方面，一是支付体系现代化缩短了资金清算占用时间；二是金融市场快速发展使得银行有更方便的融资渠道；三是银行流动性管理水平和精细化程度提高。考虑到当前超额准备金利率为0.35%（2008年12月至2020年3月为0.72%），银行主动维持较大规模超储的意愿不高，因而近年来超储率的上限并不高，在2.5%附近；其下限则在1%左右。

　　超储因其使用自由度较高，接近“银根”属性。对于银行而言，超额准备金和库存现金属于银行可动用的资金，一般情况下法定准备金被央行冻结无法动用，流通中现金则由金融体系以外的机关、团体、企事业单位和居民个人等所持有。因而，银行可动用的资金主要是超储，其次是库存现金。相对于基础货币，超储更为接近商业银行的“银根”属性。

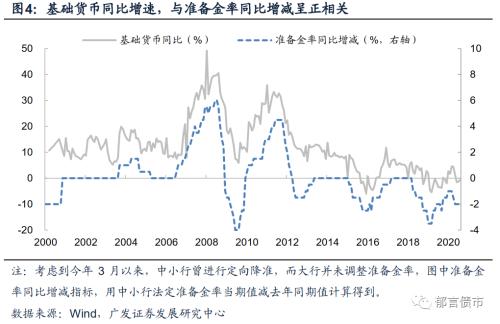
　　而基础货币的波动，主要由法定准备金率的变化所驱动。这背后的原因在于准备金存款占基础货币的比例高，在2/3左右，准备金率调整0.5%，对应法定准备金减少约8000亿元，按30万亿左右的基础货币规模，减少8000亿元相当于基础货币变动约2.7%。不过法定准备金的减少并不会完全对应基础货币减少，降准对应的准备金去向主要有两方面，一是转为超储、库存现金等仍属基础货币的科目，二是银行转作其他用途。考虑到超额准备金利率较低，而且多数时段内库存现金波动较小，大多数资金可能脱离基础货币范畴。

　　如果以基础货币指标来观察流动性，通常会发现基础货币减少，流动性反而宽松的状态；这似乎与常识相悖。原因就在于降准导致法定准备金减少，一部分转为超储使得银行可融出资金增加，另一部分脱离基础货币转为其他用途，对应基础货币减少。因而观察流动性情况，超储率要优于基础货币。

　　2

　　超储率的测算：一般方法和特殊处理

　　MLF超量续作，背后是超储率降至2017年水平MLF超量续作，背后是超储率降至2017年水平MLF超量续作，背后是超储率降至2017年水平

　　超储率测算的一般方法。以央行发布的季末月超储率为基础（假设为t月），加上估算得到的超储率月度环比变动，即可得到下一季度季初月（t+1月）和下一季度季中月（t+2月）的超储率，同样也可递推下一季度季末月（t+3月）的超储率，待延后发布该数据后进行印证。

　　例如，以央行发布今年3月超储率为基础（对应t月），加上估算的4月超储率环比变动，可得到4月超储率（t+1月），再加上估算的5月超储率环比变动，可得到5月超储率（t+2月）。在数据公布时间上，央行往往在季中月发布的货币政策执行报告中披露上一季的超储率数据，例如8月发布6月末（t+3月）的超储率。而测算时，一般是根据央行在当月披露的相关金融数据测算上月超储率，如7月中旬时具备测算6月超储率的基础数据，测算出6月超储率后。待8月央行披露该数据后，验证方法是否有效。具体方法如下：

　　超储率 + 法定准备金率 = 估算的准备金率 = 准备金存款 / 需缴准的存款。

　　对t期和t-1期取差分，得到：

　　（超储率t- 超储率t-1） + （法定准备金率t- 法定准备金率t-1）= （准备金存款 / 需缴准的存款）t- （准备金存款 / 需缴准的存款）t-1

　　其中法定准备金率、准备金存款、需缴准的存款均为已知指标。可根据货币当局资产负债表、其他存款性公司资产负债表以及存款相关的指标进行计算。从而可得出（超储率t- 超储率t-1）。根据央行公布的季末月超储率t即可向后计算超储率t+1、超储率t+2、超储率t+3。计算得到的超储率t+3，可与央行发布的下一季超储率相互印证。例如8月中旬期间，根据已发布的7月货币当局资产负债表、其他存款性公司资产负债表以及存款相关的指标，和央行发布的6月超储率数据，测算出7月超储率。到9月，则可相应测算8月超储率。

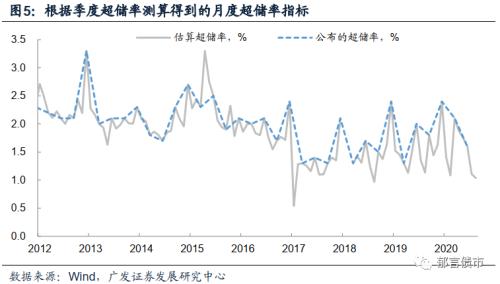
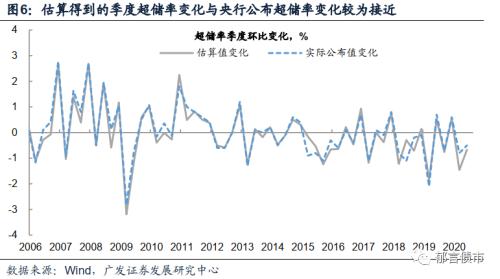
　　就理论而言，可根据t期推导至t+n期，但央行每个季度的季中月都会发布超储率，因而至多推导至t+3即可。但毕竟随着外推期数增加，偏离度将因一些特殊情况而增加（例如央行在春节前进行的TLF等特殊操作）。这也使得该方法类似于插值法，每个季度可以根据央行发布数据进行校正。根据该方法测算的超储率，6月为1.6%，7月为1.1%，8月为1.0%，详见图5。测算指标有效性，可根据测算得到的季度超储率环比变化，与央行发布的超储率环比变化相比较，见图6。可以发现该方法测算得到的指标与央行发布指标的环比变化较为接近，差距主要发生在春节所在的一季度，或定向降准期间。？

　　定向降准等情况下测算超储率的特殊处理。今年3月央行普惠金融定向降准，并未体现在法定准备金率的调整上；4月和5月针对中小银行定向降准，也仅体现为中小行法定准备金率变化，并非1月大行和中小行同步降准那样可以直接计算所有机构的法定准备金率变动。在这种情况下，测算时需要对法定准备金率变动进行还原，否则会将法定准备金率调整引起的变化，纳入到超储变化中。例如3月普惠金融定向降准释放资金5500亿元，对应准备金率变动约-0.3%，如将其纳入超储，则意味着超储会低估0.3%，应当将0.3%加回去才能得到真实的超储率。4-5月的情况也类似，分别释放2000亿元资金，对应准备金率均变动0.11%，需要分别将其加回，才能得到真实的超储率。如果不进行4-5月的调整，那么站在7月测算6月超储率，就会测算得到超储率为1.4%，而事实上应为1.6%。央行发布的数据也为1.6%。

　　与定向降准类似，央行在春节前采取的特殊措施，如TLF（临时流动性便利）、CRA（临时准备金动用安排）等也可以根据类似方法对测算超储率进行修正。

　　与五因素方法的对比：误差相对较小。传统的超储测算方法，往往根据影响超储的五大因素进行计算，思路相对更为直接。即为：

　　超储+法定准备金+货币发行=外汇占款+央行投放/回笼-财政存款

　　左侧为基础货币的储存形态，右侧为基础货币的投放（回笼）方式。可变形为：

　　超储=外汇占款+央行投放/回笼-财政存款-货币发行-法定准备金

　　央行负债端的基础货币，在储存形态上，由货币发行（流通中现金与库存现金构成）、法定准备金与超额准备金组成。在投放方式上，由资产端的外汇占款、央行公开市场操作、财政存款等来实现。根据等式右边的已知变量可以计算超储。但这种五因素绝对额估算产生的误差往往更大。从五因素方法的角度来看忽略了再贷款等因素的影响，例如今年疫情期间央行投放的再贷款，以及以往证金公司获得的再贷款，其带来的影响是不能忽略的。而我们测算方法中先计算准备金率再差分，这种求比例环比变动，可以在差分中有效规避五因素方法中其他项的扰动。这其中既包括可以获取统计数据的再贷款，也包括无法获取统计数据的其他因素。

　　根据我们剔除环比变动计算超储率时，用同一变量的不同统计指标测算得到的结论相差无几。例如准备金存款指标，既可以使用货币当局储备资产中的其他存款性公司存款，也可以使用其他存款性公司的准备金存款，计算比例变化时差距小。甚至在缺失部分指标时，也可以对超储率变动进行近似计算。例如今年9月，央行9月21日发布非银金融机构同业存款，较前几个月晚了一周左右。考虑到在此之前央行已经发布了计算所需的其他指标，忽略该指标进行测算，得到的8月超储率也可供提前参考。事实上，忽略该指标计算的8月超储率与利用该指标计算的8月超储率，其差异在小数点之后第二位，不影响超储率1.0%的测算结果。

　　3

　　超储率的应用：适合分析中期资金面

　　MLF超量续作，背后是超储率降至2017年水平MLF超量续作，背后是超储率降至2017年水平MLF超量续作，背后是超储率降至2017年水平

　　应用超储率时需要注意该指标是时点值。在利用超储率进行分析时，需要注意央行公布的超储率为季末时点值，相应地，根据货币当局资产负债表、其他存款性公司资产负债表其中的数据测算月度超储率，也为特定时点的超储率。因而根据时点值的超储率，去推断全月甚至整个季度的资金面需要谨慎。

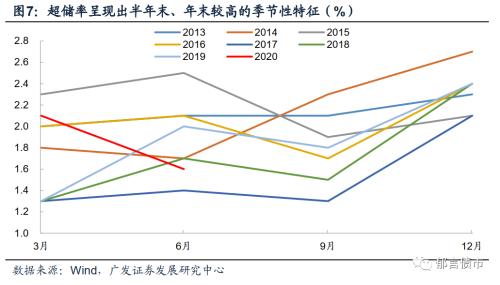
　　测算的超储率适合分析中期资金面。超储率具有季节性特征，2017年二季度货币政策执行报告的专栏一提到年中、年末超额准备金率往往会临时“鼓肚子”，主要是受到如监管考核、财政集中支出、存款变化、银行财务核算等因素影响。其中财政收支是一个重要影响因素，季初月因企业所得税预缴是收入大月（收大于支），对应央行负债端的财政存款增加，消耗超储，超储率相应降低；季末月通常是支出大月（支大于收），对应央行负债端的财政存款减少，补充超储，超储率往往较高。

　　根据超储率的季节性特征，可以将当前月份的超储率，与历史同期超储率进行比较。例如去年同期、资金面较为紧张或宽松的年份同期，可以得到中期资金面的一个初步判断。我们测算得到2020年7月、8月的超储率分别为1.1%、1.0%，与资金面较为紧张的2017年同期接近（7、8月均为1.1%），相应低于资金面较为宽松的2019年同期（7、8月分别为1.4%、1.2%）。也可以通过分析2012年以来超储率波动区间，考虑超储率存在季节性，分别计算各个季度乃至各月的超储率波动区间，将当前超储率放到历史同期超储率区间中计算分位数，从而得到当前超储率是高或低的评价。

　　测算的超储率作为月频数据，对于月内资金面的波动“束手无策”，但可以作为分析起点。根据前述测算方法，可以得到月度超储率，但月内资金面的波动却没办法由超储率的一个时点值来捕捉。依靠一个指标来完成流动性的全貌分析是不现实的。分析月内资金面的变化，需要根据影响资金面的日度数据作进一步分析，而超储率恰恰可以作为月内流动性分析的起点。以上月末的超储率，根据当月日度或周度流动性相关数据进行定量或定性的递推，即可得到反映月内当前资金面“超储率”。

　　？

　　风险提示：

　　测算超储率所使用的指标出现口径调整。