汉和资本：对投资中所谓”必然性事件“的思考

“必然性事件”指的是发生概率为100%的事件，无数的投资者都寄希望于一个模型或一套理论，寻找到价格持续稳定上涨为“必然性事件”的资产，或者简单来说价格只涨不跌的资产。

成立于1994年的长期资本管理公司聚集了一群智力超凡的天才，其中甚至还包括因提出Black-Scholes期权定价公式而获得诺贝尔经济学奖的Robert Merton和Myron Scholes。长期资本管理公司致力于通过严密的模型以及科学的计算获得稳定超额收益，事实也的确如此，他们在1994年获得了20%的收益，1995年则有43%，1996年依然维持了41%，并且期间几乎没有回撤。但是到1998年，长期资本管理公司还是倒闭了，非常不走运，他们遇到了俄罗斯金融危机，这在他们的模型中是发生概率为137亿分之一的“小概率事件”。

“小概率事件”简直就是“必然性事件”的对立面，因为小概率事件不到1%概率的存在，让必然性事件的100%概率成为了不可能。同样因为小概率事件发生的概率并非为零，这意味着小概率事件始终存在，这也让必然性事件变得并不存在。更可恶的是，日常生活或者过往的历史中，我们会发现小概率事件并不罕见，发生的概率比我们想象的更大。就像发生概率为137亿分之一的“黑天鹅”，这意味着从宇宙形成的那一刻开始，这个事件都不应该发生，却被长期资本管理公司碰上了。

肥尾效应的存在

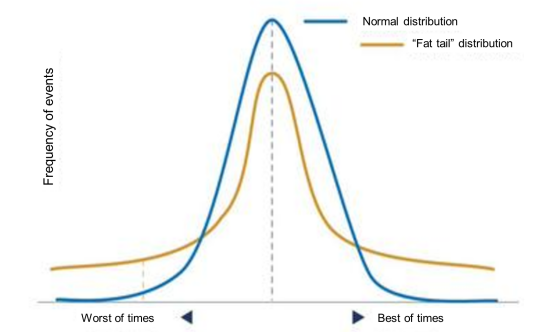
在谈“肥尾效应”之前，需要先说一下“正态分布”。正态分布又被称为高斯分布，呈现出的是钟型、两头低、中间高、左右对称的形态，也就是说大部分的数据都集中在样本平均数附近，而某个数据偏离平均数越大，发生的概率也就越小。正态分布在数学、物理、医疗等领域都是一个非常重要的概率分布模型，对于金融领域同样也是，例如Black-Scholes期权定价模型、VaR风险定价模型中都有基于正态分布模型的假设。但在现实生活中，正态分布的描述往往会出现偏差，下面这个例子可以很好的体现：

股票的收益率分布被认为是服从正态分布的，我们获取了道琼斯指数(DJI.GI)从1990年12月20日到2019年12月9日所有交易日的单日涨跌幅，共计6862个数据作为数据样本。那么按照收益率服从正态分布的假设下，我们得到所有样本的平均值为0.04%，标准差为1.08%。由此我们可以计算出：单日涨幅超过2.56%或跌幅超过2.48%发生的概率都只有1%，理论上出现的次数应该是137次;但实际情况是，过去这6862个交易日中，道琼斯指数涨幅超过2.56%或者跌幅超过2.48%的交易日出现了222次。更极端的情况是，按照正态分布来计算，单日涨幅超过5.10%或跌幅超过5.02%发生概率都应该只有百万分之一，理论上出现的次数应该是0，但实际发生的次数居然有23次。道琼斯指数的历史数据存在这样的情况并非个例，标普指数(SPX.GI)也出现了同样的情况，理论上1%的小概率涨跌幅交易日应该出现137次，实际出现227次，而理论上百万分之一概率的交易日出现次数应该是0次，实际出现了26次。

数据来源：Bloomberg

上面这个例子之所以出现这样的情况，原因就是“肥尾效应”，指的是服从正态分布的样本数据中，与样本数据平均值差异较大的数据出现的概率变大，简单来说，即分布在正态分布两侧尾部的所谓小概率事件发生的概率要比理论计算出来的大许多。股票收益率理论上符合正态分布，但实际存在肥尾效应，因此实际极端涨跌幅出现的概率比理论计算更大。

事件之间的关联性

有一道经典的概率计算题，即有三颗骰子，求三颗骰子同时掷出6的概率。这道题目非常简单，很容易算出答案就是1/216，因为每个骰子掷出6的概率都是1/6，直接相乘就可以得到答案。这个问题能这样计算的先决条件是三颗骰子的投掷都是独立事件，即事件之间互无联系，但现实生活中大部分事件都是相互关联的，即使表面上不易被察觉。

二十一世纪初，美国受到互联网泡沫破灭以及911事件的影响，经济增速大幅放缓，美国政府为了推动经济，连续通过法案刺激人们购房，刺激银行向低信用群体提供贷款，也就是所谓的次级贷款。次级贷款本身的信用评级堪比垃圾债券，而贷款公司希望将次级贷款卖出去，不仅可以获得现金同时可以转移风险。低评级的次级贷款并不容易找到买家，于是贷款公司想了个方法，将这些CCC评级的次级贷款打包，摇身一变成为一个AA的资产包，就可以顺利卖出去了。那么为什么评级公司愿意给垃圾资产组成的资产包一个高评级呢?原因在于评级师们认为虽然都是次级贷款，但是贷款人的年龄、职业、所在地等等都不一样，相互之间没有关联性，因此同时发生违约的可能性很小。如果从数学的角度来看，资产包内的每笔次级贷款发生违约都是“独立事件”，假设每个次级贷款人发生违约的概率是10%，那么10个次级贷款同时发生违约的概率就是一百亿分之一，也就是说整个次级贷款包发生违约是”极小概率事件“。但倾巢之下安有完卵，随着经济走差、失业率整体提高的时候，底特律的汽车工人和迈阿密的餐馆服务生很可能同时发生违约。次级贷款资产包中每笔次级贷款发生违约绝非独立的无关联的事件，而资产包发生违约的概率也远大于计算获得的结果。

现实世界绝非一道数学题可以表述，或者一个条件可以定义。生活中的绝大部分事件都是不相互独立的，即使表面看着毫不相关的两件事情也可能存在深层次的联系。简单通过计算就认定一件事情是小概率事件不过也是自欺欺人。

经验缺失的影响

现实生活中并非所有的概率问题都有充分的先决条件。例如已知袋子里白球和黑球的个数，要求计算摸出黑球的概率。这很容易;但如果不知道袋子里有几个黑球和几个白球，而是要根据取出球的颜色判断袋子里黑白球的比例，这个问题再用经典的概率论方法就无法解决了。往往生活中的问题与后者更加类似。

贝叶斯在18世纪70年代提出了“贝叶斯定理”，可以用来解决这些逆向概率的问题。如今贝叶斯定理在例如保险业、银行业当中的应用非常普遍。那么贝叶斯定理是怎么计算概率的呢?

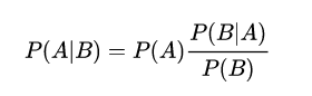
上图就是贝叶斯公式，我们把P(A|B)称为“后验概率”，也就是我们要计算的概率;P(A)称为“先验概率”，代表的是在缺少先决条件下借助经验主观判断的概率;而P(A)后面的部分可以理解为“调整因子”，是新增信息B对先验概率的修正，当然新增信息可能不止一个B，不断增加的新增信息会对先验概率进行不断的修正。简单来说，贝叶斯定理计算概率的方式就是先给出一个经验概率，然后再不断的通过新增信息去验证和修正这个概率。

回到开始的那个问题，在不知道袋子里黑球和白球个数的情况下，如何确认白球和黑球的比例?那最先开始的时候先假设黑白球的比例分别为50%，而后在每次取出球的时候再修正这个概率，如果取到第10颗球，结果是有3颗黑球，7颗白球，那么后验概率也将被修正为黑球比例为30%，白球比例为70%。

贝叶斯定理的缺陷在于，当调整因子有限的情况下，严重依赖于先验概率，而先验概率又严重依赖于判断者的经验，就像以上例子中初始判断白球和黑球的比例各为50%也不是一个3岁小孩能判断的。对于小概率事件来说，本身发生的次数就极少，因此判断者的相关经验十分缺失，或者说在小概率事件面前就像3岁小孩一样，导致的结果就是先验概率被低估，使得计算出来的概率低于事件实际发生的概率。

因为肥尾效应的存在，事件之间总有不易察觉的关联性，以及贝叶斯定理严重依赖于经验等原因，小概率事件无法避免且比我们想象中发生的可能性更大，这意味着投资中所谓价格持续上涨为“必然性事件”的资产是不存在的。但是投资中是否存在“必然性原理”呢?答案是肯定的，那便是资产价格始终围绕资产价值波动。

如何理解资产价格始终围绕资产价值波动

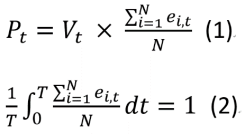
上面公式表示了特定时点价格资产价格的形成机制。公式(1)中Pt代表着t时刻的资产价格，Vt代表着t时刻的资产价值，Vt后面这一部分我们定义为影响资产价格的市场影响因子。影响因子中的N代表着市场上的N个投资者，ei,t代表着每个投资者在t时刻的主观判断力，因此整个影响因子实际上表示的就是市场中所有投资者在t时刻主观判断力的均值。公式(2)表示在T时间段内，市场影响因子的平均值为1，也就意味着在T时间段内P的均值是等于V的均值的。

简单来说，在不同的时刻每个投资者都会因为自身的一些原因产生对同一资产不同的看法，可能乐观也可能悲观，而整个市场对这一资产的看法就是市场中所有投资者看法的汇总，因而资产的价格会受到这一时刻市场整体看法的影响。但是长期来看，市场整体看法对资产价值并没有影响，资产的价格长期看是能反映其价值的。

更进一步来说，到底是什么影响了公式中的P，或者说到底是什么影响了资产的价格?那便是公式中的V，也就是资产的价值。

如何利用资产价格始终围绕资产价值波动

如果理解了资产价格始终围绕资产价值波动这一必然性原理的机制，理解了长期看市场情绪并不会影响资产价格，以及真正影响资产价格的是资产价值。那么结论就十分显而易见，那便是坚持“长期价值投资”。坚持长期价值投资并不等同于找到价格只涨不跌的资产，但可以让投资者专注于资产价值的变化，忽略短期的市场扰动以及抵御小概率事件的影响。

如果坚持长期价值投资，那么我们会发现文中第一部分的三点的影响，不论是肥尾效应、还是事件关联性、亦或贝叶斯定理对经验的依赖，都可以忽略不计。

即使从道琼斯指数以及标普指数的历史数据可以发现其单日收益率未完全符合正态分布而存在肥尾效应，但如果长期持有，依然可以享受平均每个交易日0.04%的正收益。

即使2008年因分析师忽略了次级贷款人相互之间的深层次关联性而产生金融危机，但如果长期持有，依然可以享受之后美股长达10年的上涨。

即使贝叶斯定理中严重依赖于经验，因而导致早期判断的偏差，但如果长期持有，依然可以在持续的跟踪当中去增加调整因子以不断的修正先验概率，并使得后验概率向准确值不断趋近。

写在最后：

投资中不存在所谓价格持续上涨为“必然性事件”的资产，但站在更高的层面来看，投资中却有“必然性原理”，那便是资产价格始终围绕资产价值波动。如何理解这一必然性原理很重要，但在理解之后如何加之以利用更为关键。坚持长期价值投资便是将这一必然性原理充分利用的有效方法，可以帮助我们忽略市场情绪以及小概率事件的短期扰动，专注于资产价值的兑现。投资中如此，生活中亦如此。坚持长期做正确的事情，短期内虽然可能起起落落，但长期终将通向光明。

声明：

北京汉和汉华资本管理有限公司不对本文中提及的任何一家公司或行业进行评价、预测及推荐，本文仅使用历史实际数据进行观点论述，不构成任何投资建议。

本文章版权为北京汉和汉华资本管理有限公司所有，数据来源：Bloomberg。任何媒体、网站或个人未经本公司授权不得以转载、链接、转贴或以其他方式复制发布/发表。已经本公司授权的媒体、网站或个人在引用时需注明出处为“汉和资本”，且不得对本文进行有悖原意的引用、删节和修改。本公司保留追究法律责任的权利。